Preprint 2026

Meta Flow Maps enable scalable reward alignment

Peter Potaptchik*, Adhi Saravanan*, Abbas Mammadov, Alvaro Prat, Michael S. Albergo†, Yee Whye Teh†

University of Oxford · Harvard University · Kempner Institute

Overview

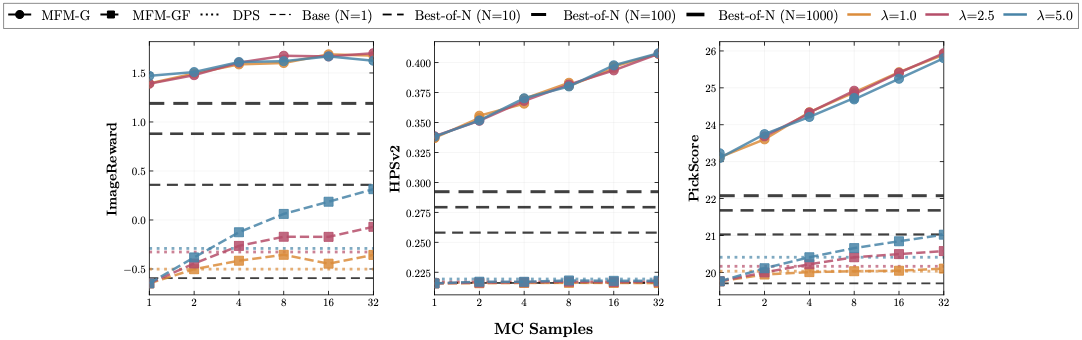
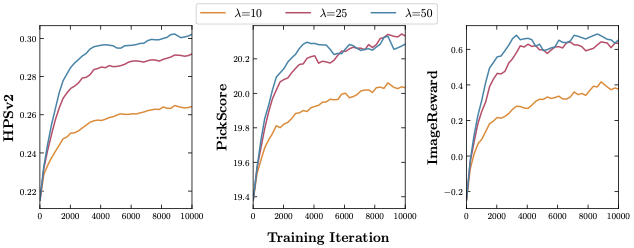
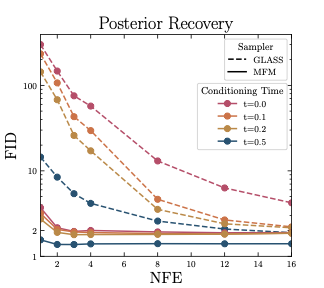
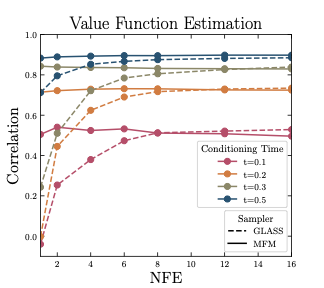
Controlling generative models is computationally expensive. Optimal alignment with a reward function requires estimating the value function, which demands access to the conditional distribution of data given a noisy sample $p_{1|t}(x_1|x_t)$—typically requiring costly trajectory simulations. We introduce Meta Flow Maps (MFMs), extending consistency models and flow maps into the stochastic regime. MFMs perform one-step posterior sampling, generating i.i.d. draws of clean data from any intermediate state with a differentiable reparametrization for efficient value function estimation. This enables inference-time steering without rollouts and unbiased off-policy fine-tuning. Our steered-MFM sampler outperforms Best-of-1000 on ImageNet at a fraction of the compute.

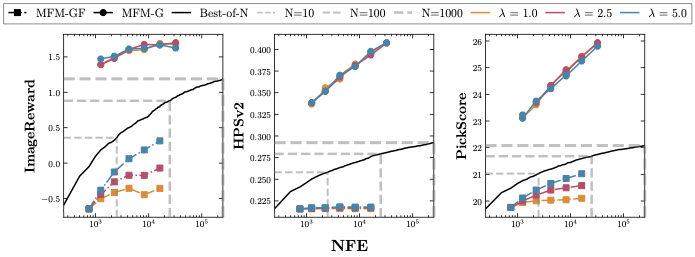
Compute-normalized performance: MFM steering achieves better reward scores with fewer function evaluations

MFM steering achieves higher rewards with >100× fewer function evaluations than Best-of-N.

Motivation

Modern generative models like diffusion and flow-based models produce stunning samples, but controlling them remains a core challenge. Whether we want to steer generation toward high-reward outputs at inference time, or permanently fine-tune a model to align with human preferences, we face the same fundamental bottleneck: estimating the value function.

The value function tells us how good a noisy intermediate state is—but computing it requires sampling from the conditional posterior: the distribution of all possible clean outputs consistent with that noisy state. Existing methods either approximate this posterior crudely (introducing bias) or simulate expensive trajectories (killing efficiency).

Meta Flow Maps solve this dilemma by learning to sample the full posterior in a single forward pass, enabling both efficient steering and unbiased fine-tuning.

Core Contributions

Meta Flow Maps (MFMs): Stochastic extensions of consistency models and flow maps that generate arbitrarily many one-step samples of clean data x₁ conditioned on any noisy state x_t.
Full Posterior Capture: Unlike standard few-step models, MFMs capture the full conditional posterior p_1|t(·|x_t), not just a point estimate.
Inference-Time Steering: We leverage these differentiable samples for efficient, asymptotically exact inference-time steering via Monte Carlo estimators of the value function gradient.
Off-Policy Fine-Tuning: MFMs enable efficient off-policy fine-tuning to general rewards using unbiased objectives, without tricky on-policy simulation.

The Key Idea

Meta Flow Map Diagram showing how MFMs map noise to posterior samples

An MFM conditions on an intermediate time–state pair $(t, x)$ and learns a shared conditional flow that maps base noise $\varepsilon$ to endpoint samples $x_1$ from the posterior $p_{1|t}(\cdot|x)$. Varying the initial noise yields multiple i.i.d. samples from the same posterior.

Stochastic Flow Map

A function $\Phi(\varepsilon; c)$ that maps base noise $\varepsilon$ (gray squares on the left) to samples from a target distribution $p_c$, indexed by a context $c$:

\Phi(\cdot\,; c) \# q = p_c, \quad \forall c \in \mathcal{C}

The context $c$ "selects" which distribution to sample from.

Meta Flow Map

Here the context is $(t, x)$—a time and noisy image (e.g., the blurry dog at $(t_a, x_a)$). The MFM $X_{0,1}(\varepsilon; t, x)$ maps noise to clean images consistent with that noisy state:

X_{0,1}(\varepsilon; t, x) \sim p_{1|t}(\cdot|x)

The clean dogs on the right are i.i.d. samples from $p_{1|t_a}(\cdot|x_a)$—different noise $\varepsilon, \varepsilon'$ yields different valid reconstructions.

Key insight: The stochastic interpolant defines an infinite family of conditional posteriors $p_{1|t}(\cdot|x)$—one for each time–state pair $(t,x)$ drawn from the law of the interpolant itself. Each posterior has a corresponding ODE that transports noise to it, and each such ODE has a flow map compressing its trajectories to a single step. A Meta Flow Map learns to select from this infinite collection: given context $(t_a, x_a)$ (noisy dog), it picks the flow map for the dog posterior; given $(t_b, x_b)$ (noisy flower), it picks the flower posterior—all via the same learned network $X_{0,1}$. Because the MFM is a differentiable function along the law of interpolant, we can exploit its differentiability in the estimation of the value function gradient.

Results

MFMs achieve competitive sample quality while enabling efficient reward alignment on ImageNet 256×256.

Sample Gallery

Base MFM Samples (4-step)

lion

tiger

macaw

toucan

giant panda

bald eagle

Steering: "majestic volcano erupting with lava"

Base MFM

→

Steered MFM

The base MFM uses only class labels. All prompt alignment comes from HPSv2 steering.

Steering: "ginger tabby cat"

Base MFM

→

Steered MFM

Steering with HPSv2 reward model transforms class-conditioned outputs to match text prompts.

Steering: "space shuttle launching, fiery fumes"

Base MFM

→

Steered MFM

MFM steering enables precise control without retraining the base model.

Fine-tuning: Samples at λ = 10, 25, 50

Samples before and after fine-tuning with MFM-FT. Shown across tilt scales λ .

Fine-tuning: Samples at λ = 10, 25, 50

Our MFM-FT fine-tuning objective is off-policy and unbiased. Samples shown across different tilt scales λ.

Steering: Base vs. HPSv2-Steered with MFM-G

Base MFM samples (top rows) versus HPSv2-steered samples using MFM-G (bottom rows) across different number of MC samples.

Quantitative Results

Steering Performance Across Reward Models

MFM-G outperforms Best-of-1000 across ImageReward, HPSv2, and PickScore reward models.

Compute-Normalized Performance

MFM steering achieves better reward scores with >100× fewer function evaluations than Best-of-N.

Fine-Tuning with HPSv2

Stable reward improvements across HPSv2, ImageReward, and PickScore during fine-tuning, with no reward hacking.

Posterior Recovery Quality

Left: Posterior FID across conditioning times. Right: Value function estimation correlation. MFMs strongly outperform ODE rollouts.

Citation

@article{potaptchik2025metaflowmaps,
  title={Meta Flow Maps enable scalable reward alignment},
  author={Potaptchik, Peter and Saravanan, Adhi and 
          Mammadov, Abbas and Prat, Alvaro and 
          Albergo, Michael S. and Teh, Yee Whye},
  journal={arXiv preprint},
  year={2025}
}